「Algorithm4」3: Searching

30 Dec 2023

Official Website: https://algs4.cs.princeton.edu/home/

Searching

Searching is the process of efficiently locating a specific element within a collection of data. In the age of modern computers and networks, where we have access to vast amounts of information, efficient searching is critically important. This chapter will introduce several classic search algorithms.

The Symbol Table (or Dictionary) is an abstract data structure that formalizes the concept of searching. Its primary purpose is to associate a key with a value, allowing for quick access to the value by its key. There are various ways to implement a symbol table, such as binary search trees, red-black trees, and hash tables. This chapter will focus on these tree-based implementations.

Note: The C++ implementations of the search algorithms discussed can be found in this GitHub repository.

Sequential Search Symbol Table (Unordered Linked List)

This is the simplest implementation of a symbol table. We can use a linked list to store the data. When we need to retrieve an element, we simply traverse the list from the beginning.

template <typename KEY, typename VALUE>
class SequentialSearchSymbolTable {
public:
    ~SequentialSearchSymbolTable() {
        while (head_ != nullptr) {
            Node* old = head_;
            head_ = head_->next;
            delete old;
        }
    }

    void put(KEY key, VALUE value) {
        for (Node* x = head_; x != nullptr; x = x->next) {
            if (x->key == key) {
                x->value = value;
                return;
            }
        }
        head_ = new Node(key, value, head_);
        size_++;
    }

    std::optional<VALUE> get(KEY key) {
        for (Node* x = head_; x != nullptr; x = x->next) {
            if (x->key == key) {
                return x->value;
            }
        }
        return std::nullopt;
    }

    void remove(KEY key) {
        Node* previous = nullptr;
        for (Node* x = head_; x != nullptr; previous = x, x = x->next) {
            if (x->key == key) {
                if (previous != nullptr) {
                    previous->next = x->next;
                } else {
                    head_ = x->next;
                }
                delete x;
                size_--;
                return;
            }
        }
    }

    bool contains(KEY key) { return get(key).has_value(); }
    bool is_empty() { return head_ == nullptr; }
    size_t size() { return size_;}

private:
    struct Node {
        KEY key;
        VALUE value;
        Node* next;
        Node(KEY key, VALUE value, Node* next) : key(key), value(value), next(next) {}
    };

    Node* head_ = nullptr;
    size_t size_ = 0;
};

The C++ code above provides a simple implementation of a sequential search symbol table. It uses a private inner Node class to represent the linked list nodes that store the KEY and VALUE. Both the get and put methods perform a linear scan of the list to find the given key.

While this implementation works, it is relatively inefficient. The get and put methods have a time complexity of (O(N)), making them unsuitable for large-scale problems.

Binary Search Symbol Table (Ordered Array)

This implementation is also relatively straightforward. It uses a pair of parallel arrays to store keys and values, respectively. Data insertion and retrieval are handled using binary search, which requires the keys to be kept in sorted order.

By replacing linear traversal with binary search, this implementation optimizes the get method’s complexity to (O(\log N)).

template<Comparable KEY, typename VALUE>
class BinarySearchSymbolTable {
public:
    void put(KEY key, VALUE value) {
        int i = rank(key);
        if (i < keys_.size() && keys_[i] == key) {
            values_[i] = value;
            return;
        }
        keys_.insert(keys_.begin() + i, key);
        values_.insert(values_.begin() + i, value);
    }

    std::optional<VALUE> get(KEY key) {
        if (is_empty()) return std::nullopt;
        int i = rank(key);
        if (i < keys_.size() && keys_[i] == key) {
            return values_[i];
        }
        return std::nullopt;
    }

    void remove(KEY key) {
        if (is_empty()) return;
        int i = rank(key);
        if (i < keys_.size() && keys_[i] == key) {
            keys_.erase(keys_.begin() + i);
            values_.erase(values_.begin() + i);
        }
    }

    // returns the number of keys in this symbol table strictly less than key.
    int rank(KEY key) {
        int left = 0, right = keys_.size() - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2; // prevent integer overflow
            if (key < keys_[mid]) {
                right = mid - 1;
            } else if (key > keys_[mid]) {
                left = mid + 1;
            } else {
                return mid;
            }
        }
        return left;
    }

    std::optional<KEY> min() {
        if (is_empty()) return std::nullopt;
        return keys_.front();
    }

    std::optional<KEY> max() {
        if (is_empty()) return std::nullopt;
        return keys_.back();
    }

    std::optional<KEY> select(int k) {
        if (k < 0 || k >= keys_.size()) return std::nullopt;
        return keys_[k];
    }

    std::optional<KEY> ceiling(KEY key) { return select(rank(key)); }

    std::optional<KEY> floor(KEY key) { return select(rank(key) - 1); }

    bool contains(KEY key) { return get(key).has_value(); }

    bool is_empty() { return keys_.empty(); }

    size_t size() { return keys_.size(); }

private:
    std::vector<KEY> keys_;
    std::vector<VALUE> values_;
};

Binary Search Trees (BSTs)

In the previous implementation, using an ordered array optimized search speed, but because binary search requires a sorted array, the put method’s efficiency is unsatisfactory (due to shifting elements). We might need a linked structure to make insertions faster. How can we apply the principles of binary search to a linked structure? This is where the Binary Search Tree (BST) comes in.

A Binary Search Tree (BST) is a binary tree where the key in each node is greater than any key in its left subtree and less than any key in its right subtree.

Deleting the Minimum Node

Find the minimum node by repeatedly traversing to the left child until a node with a null left child is found.
If this minimum node has a right child, update the parent’s left link to point to the minimum node’s right child.

Deleting an Arbitrary Node

Find the node to be deleted, t.
Find t’s successor, x, which is the minimum node in t’s right subtree. This node x will take t’s place.
In t’s right subtree, perform the “delete minimum” operation to remove x.
Set x’s right child to be t’s (now modified) right subtree.
Set x’s left child to be t’s left child.

Balanced Search Trees

The efficiency of a standard BST heavily depends on the randomness of the input data. If the input is not random (e.g., already sorted), the resulting tree can become severely “unbalanced,” degrading performance to that of a linked list. Some implementations use specific techniques to adjust the tree’s structure, ensuring it remains balanced regardless of the input order.

2-3 Trees

A 2-3 tree is a type of search tree that allows nodes to hold more than one key, which helps maintain balance. It consists of two types of nodes:

2-node: One key and two children (for keys < key and > key).
3-node: Two keys and three children (for keys < key1, > key1 & < key2, and > key2).

A key property of a 2-3 tree is that it is always perfectly balanced, meaning the path from the root to every null link is of the same length.

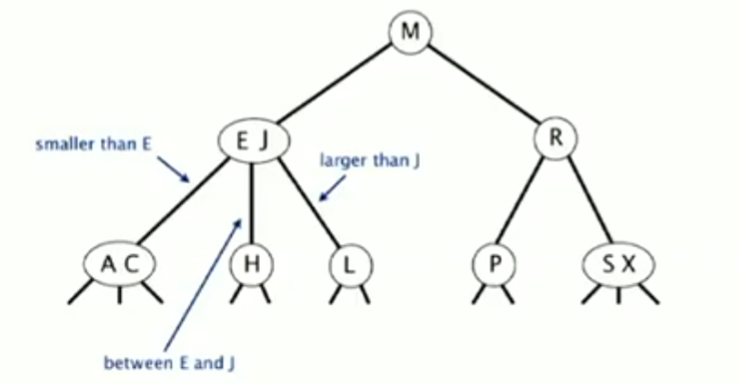
Searching in a 2-3 tree is similar to a standard BST. Insertion, however, is more involved. We first search for the appropriate insertion point at the bottom of the tree. The action taken depends on the type of node we land on:

Case 1: Inserting into a 2-node
- The new element is added to the 2-node, converting it into a 3-node.
Case 2: Inserting into a 3-node
- The new element is temporarily added, creating a temporary 4-node (with three keys).
- This 4-node is split: the middle key moves up to the parent node, and the remaining two keys form two new 2-nodes.
- If the parent node was already a 3-node, this splitting process is repeated up the tree.

In a 2-3 tree, the tree’s height only increases when the root node splits. Unlike a standard BST, a 2-3 tree grows from the bottom up.

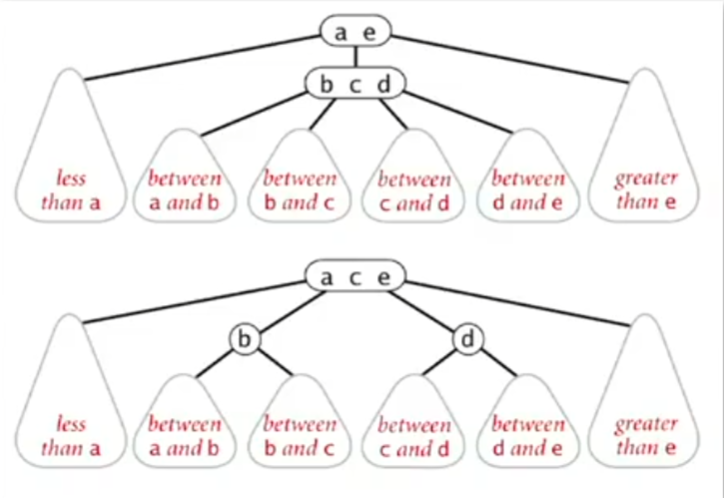
Red-Black BSTs

A red-black tree is a clever way to represent a 2-3 tree using a standard binary tree. We represent 3-nodes by splitting them into two 2-nodes connected by a special “red” link.

In a Left-Leaning Red-Black Tree (LLRBT), we represent a 3-node using a left-leaning link. The link connecting the two keys of the original 3-node is colored red, while all other links are black. This coloring allows us to maintain the properties of the 2-3 tree.

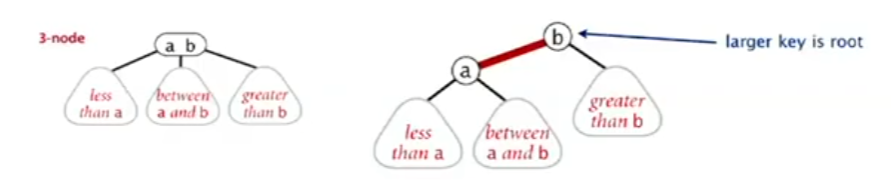
Using this scheme, any 2-3 tree can be uniquely represented as a red-black BST.

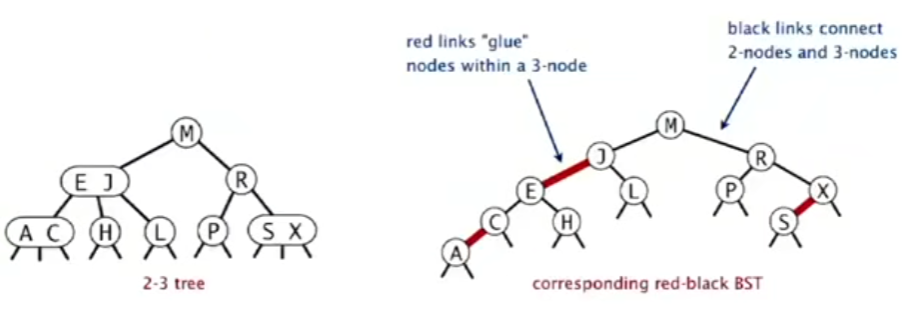
Properties of a Left-Leaning Red-Black Tree

No node is connected to two red links.
The number of black links on any path from the root to a null link is the same (perfect black balance).
Red links always lean left.

Search

Searching in a red-black tree is identical to searching in a standard BST; the colors are ignored during the search. The advantage of red-black trees is that they achieve balance without altering the fundamental search algorithm of a BST.

Representing Colors

In a practical implementation, we don’t explicitly create ‘link’ objects. Since each node in a binary tree is referenced by only one parent, we can store the color of the link pointing to a node within the node itself.

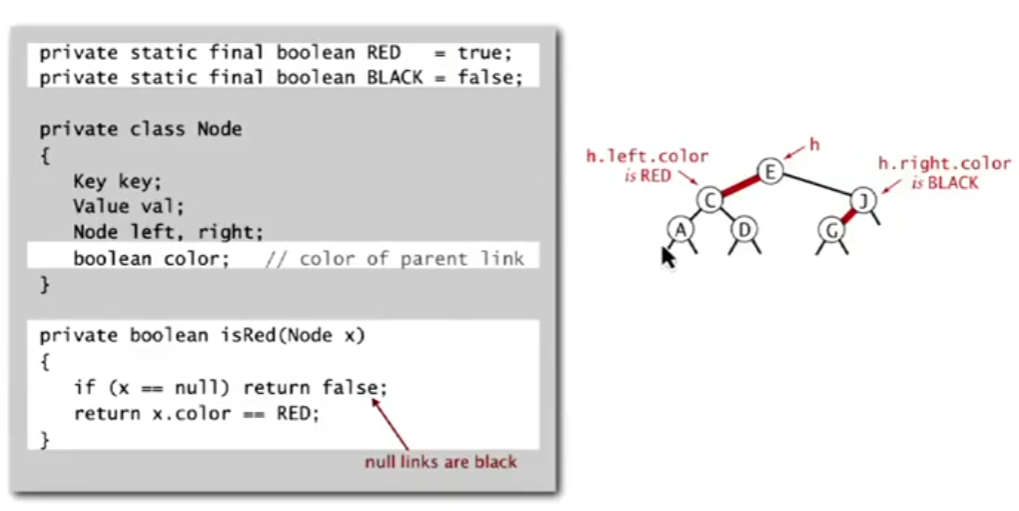
In the example above, the link from E to C is red, so we store the red color property in node C. By convention, all null links are considered black.

Three Fundamental Operations

To maintain the red-black properties during insertion and deletion, we use three core operations:

Left Rotation: Takes a right-leaning red link and converts it to a left-leaning one.

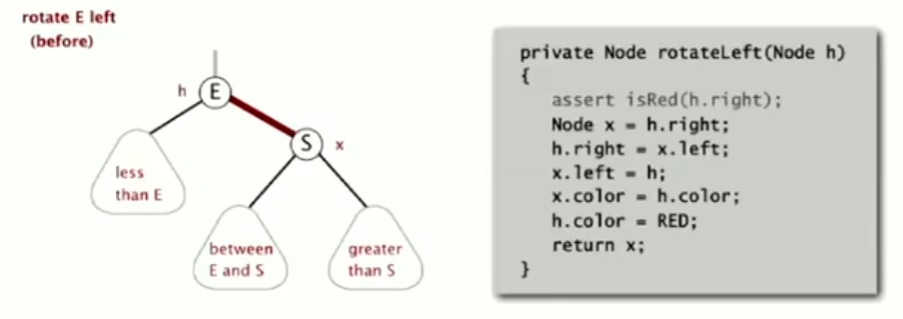
Right Rotation: The inverse of a left rotation. Even in a LLRBT, we sometimes need to temporarily create right-leaning links during rebalancing.

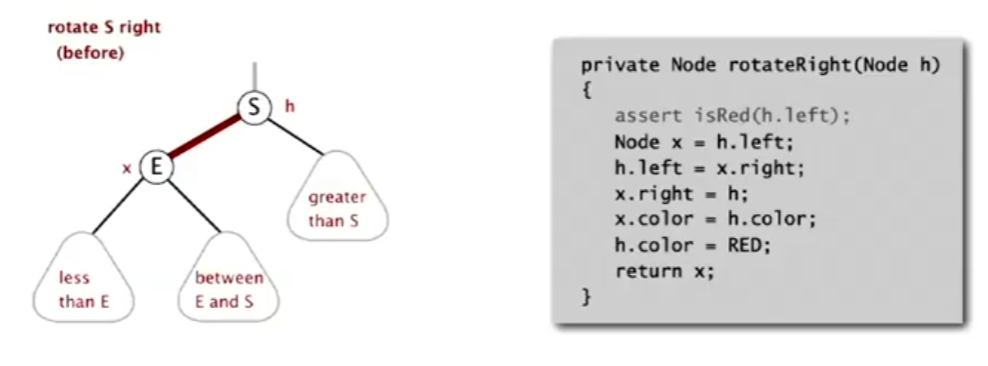
Note that rotations do not change the inorder traversal of the nodes (the relative order of keys) or violate the black balance. They are purely restructuring tools.

Color Flip: This operation simulates the splitting of a 4-node in a 2-3 tree. In a red-black tree, this is achieved simply by changing the colors of a node and its two children.

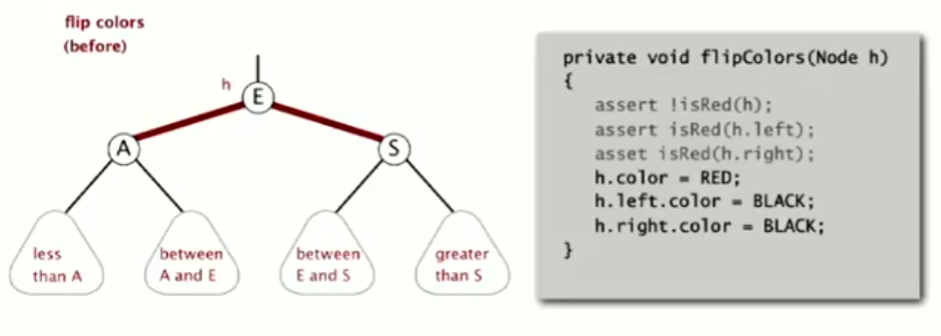
Changing the links from E to A and E to S to black simulates the split. Changing E’s incoming link to red simulates promoting the middle key (E) to its parent.

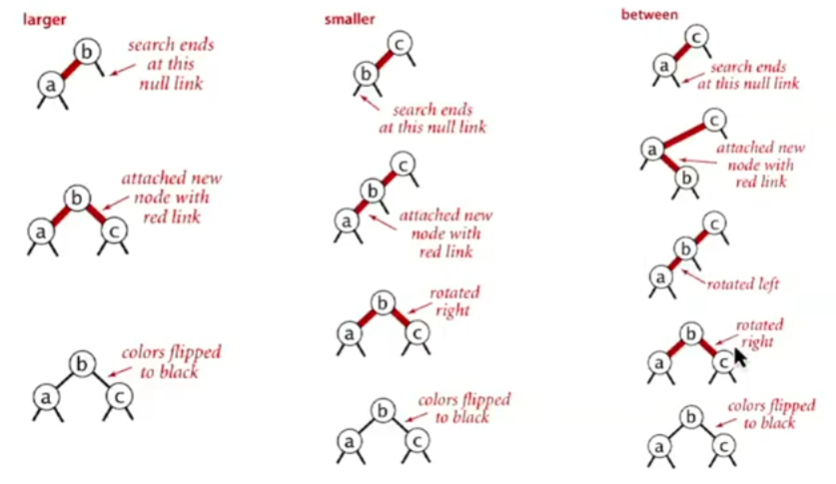
Insertion

The basic strategy for insertion is to use the three fundamental operations above to simulate the insertion process in a 2-3 tree.

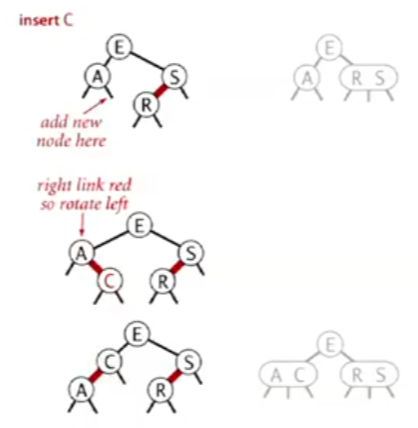
Inserting into a 2-node at the bottom:
- Perform a standard BST insertion, and color the new link (and thus the new node) red.
- If this creates a right-leaning red link, perform a left rotation to fix it.

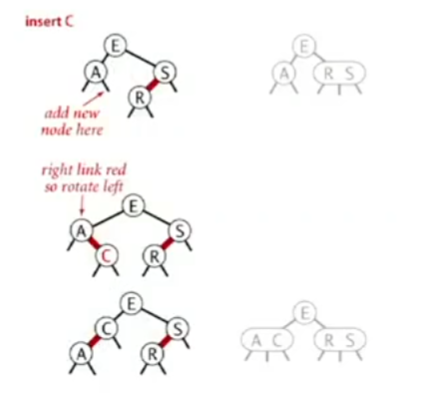
Inserting into a 3-node at the bottom:
- Perform a standard BST insertion, coloring the new node red. This temporarily creates a 4-node.
- Rotate to balance the 4-node if necessary.
- Perform a color flip to split the 4-node, passing the red link up the tree.
- Rotate to fix any resulting right-leaning links.

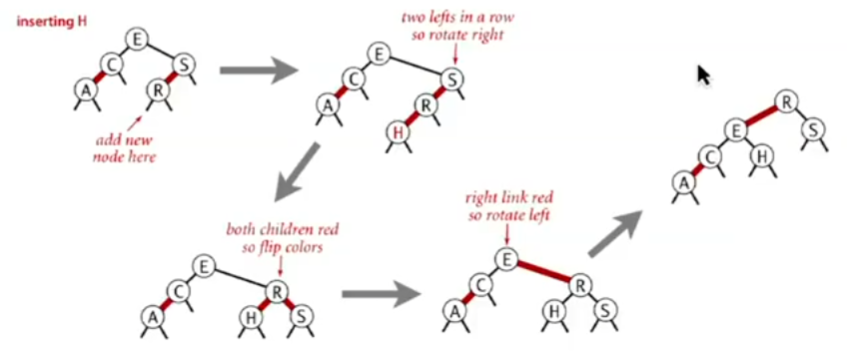
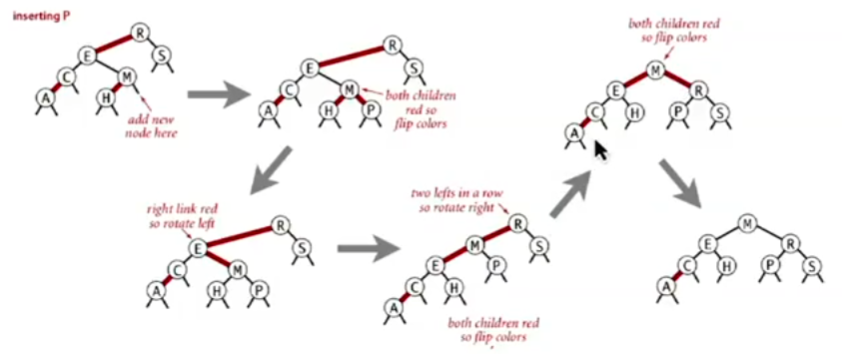
The following diagram shows a case analysis for inserting a node into a tree with two existing nodes. The general process described above is derived from these cases.

Recursive Application:
- If the tree properties are violated higher up after an insertion and rebalancing, repeat Case 1 or Case 2. This is typically handled recursively as we move back up the tree from the insertion point.

A Simple C++ Implementation

template<Comparable KEY, typename VALUE>
class RedBlackBST {
private:
    struct Node {
        KEY key;
        VALUE value;
        Node *left;
        Node *right;
        bool is_red;

        Node(KEY k, VALUE v, bool red = true)
            : key(k), value(v), left(nullptr), right(nullptr), is_red(red) {}
    };

    Node *root_ = nullptr;

    bool is_red(Node *node) const {
        if (node == nullptr) return false;
        return node->is_red;
    }

    Node* rotateLeft(Node *h) {
        assert(h != nullptr && is_red(h->right));
        Node* x = h->right;
        h->right = x->left;
        x->left = h;
        x->is_red = h->is_red;
        h->is_red = true;
        return x;
    }

    Node* rotateRight(Node *h) {
        assert(h != nullptr && is_red(h->left));
        Node* x = h->left;
        h->left = x->right;
        x->right = h;
        x->is_red = h->is_red;
        h->is_red = true;
        return x;
    }

    void flipColor(Node *h) {
        assert(h != nullptr && h->left != nullptr && h->right != nullptr);
        assert(!is_red(h) && is_red(h->left) && is_red(h->right));
        h->is_red = true;
        h->left->is_red = false;
        h->right->is_red = false;
    }

    Node* put(Node *h, KEY key, VALUE value) {
        if (h == nullptr) return new Node(key, value, true);

        if (key < h->key)		h->left = put(h->left, key, value);
        else if (key > h->key)	h->right = put(h->right, key, value);
        else					h->value = value;

        if (is_red(h->right) && !is_red(h->left)) 		h = rotateLeft(h);
        if (is_red(h->left) && is_red(h->left->left)) 	h = rotateRight(h);
        if (is_red(h->left) && is_red(h->right)) 		flipColor(h);

        return h;
    }

    const Node* get(Node *h, const KEY& key) const {
        while (h != nullptr) {
            if (key < h->key)		h = h->left;
            else if (key > h->key)	h = h->right;
            else					return h;
        }
        return nullptr;
    }

public:
    bool is_empty() const {
        return root_ == nullptr;
    }

    void put(KEY key, VALUE value) {
        root_ = put(root_, key, value);
        root_->is_red = false;
    }

    std::optional<VALUE> get(const KEY& key) const {
        const Node* res = get(root_, key);
        if (res == nullptr) return std::nullopt;
        return res->value;
    }
};